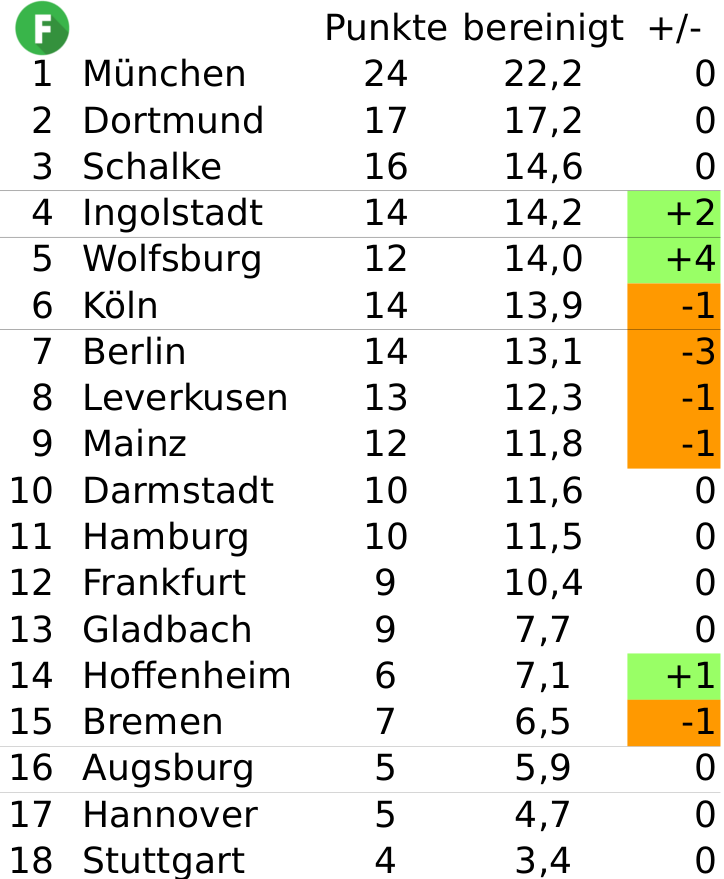
In der Tabelle gilt: Ein Punkt ist ein Punkt ist ein Punkt. Ingolstadt und Hertha sind punktgleich. Beide haben zweimal Unentschieden gespielt, dafür beide 2 Punkte erhalten. Aber Hertha hat gegen Bremen und in Frankfurt remisiert, für Ingolstadt hießen die ungleich potenteren Gegner Wolfsburg und Köln. Ist das nichts wert? Die Tabelle sagt: »Nein!«. Ich werde in diesem Artikel eine neue Art von Tabelle einführen, die »Doch!« sagt.
Natürlich lügt eine Tabelle selbst nicht. Sie entsteht, indem man alle ausgespielten Ergebnisse zu Grunde legt und daraus auf die bewährte, nachvollziehbare Weise eine Rangordnung der Mannschaften erstellt, die nebenbei und zur feineren Sortierung Größen wie die Gesamtzahl geschossener und kassierter Tore ausgibt. Trotzdem ist sie nicht vollkommen, nicht ausgenommen von jeder Kritik.
»Wir schauen nicht auf die Tabelle – die hat erst ab dem zehnten Spieltag Aussagekraft« – Ralf Rangnick
Zwei Gründe für diese Einschätzung liegen auf der Hand: Zum einen wirken sich Spiele oder Phasen von besonderem Glück, Pech oder außergewöhnlicher Formschwäche gravierender aus, je weniger Partien gespielt sind: Angesichts der offenkundigen Schwächephase zu Saisonbeginn würde kaum jemand das aktuelle Leistungsvermögen von Borussia Mönchengladbach an ihrer Tabellenplatzierung messen.
Zum anderen hängt die eigene Punktausbeute immer auch von den gegnerischen Mannschaften ab, gegen die jene Punkte erbeutet wurden. Werderfans können ein Lied davon singen: Nach Siegen gegen die außer Form befindlichen Teams aus Gladbach und Hoffenheim und dem zwischenzeitlichen sechsten Tabellenplatz sah Thomas Eichin die Mannschaft für den Kampf um die internationalen Plätze gerüstet – es folgten vier Niederlagen am Stück.
Aber nicht umsonst spielt im Laufe der Saison jeder genau zweimal gegen jeden, bevor abgerechnet wird. Man misst der Tabelle nach einem Spieltag nicht allzu viel Bedeutung bei – und vor dem letzten Spieltag achtet man bei der Abschätzung der Chancen im Abstiegskampf genau darauf, wer auswärts in Dortmund und wer in Augsburg antreten muss. Mitten in der Saison fällt diese Einordnung der Tabelle in den Spielplan schwerer – Programme aus acht gespielten Teams lassen sich natürlich nicht so leicht miteinander vergleichen wie das eine erledigte bzw. verbleibende Duell am ersten/letzten Spieltag. Was tun?
Man kann sich zunächst einmal ansehen, durch welche Siege eine Punktzahl zu Stande gekommen ist. Die folgende Visualisierung nach vier Spieltagen zeigt per Pfeil an, wer wen geschlagen hat. Dabei wird jedes Team so platziert, dass es höher als alle bezwungenen Gegner steht.
Eine Hierarchie nach vier Spieltagen
In dieser Ansicht werden alle Unentschieden und alle noch nicht gespielten Partien ignoriert, es fließen nur die Begegnungen mit Sieger und Verlierer mit ein. Selbstverständlich ist dies nur eine mögliche Ansicht, die ebenso wenig wie die Tabelle eine in Stein gemeißelte Hierarchie der Mannschaftsstärken darstellt. Verzerrende Effekte gibt es auch hier: So steht Wolfsburg mit nur zwei Siegen zwei Ebenen höher als die viermal siegreichen Münchner – dank der guten Bilanz der bezwungenen Schalker und Frankfurter.
Aber selbst wenn man darüber hinwegsieht: Man kann die Teams in einem solchen Schema nur dann übereinander platzieren, wenn sich keine »Kreise« ergeben, wie es inzwischen, nach acht Spieltagen, der Fall ist:
Wenn es solche Pfeile im Kreis gibt, kann das obige Schema nicht aufrecht erhalten werden, da in jedem Kreis mindestens ein Pfeil nach oben zeigen müsste, also mindestens ein Besiegter über seinem Besieger stünde. Die Idee, Mannschaften an der Stärke der bisherigen Gegner zu messen, lässt sich aber auch auf andere Weise umsetzen.
Es soll im Folgenden eine neue Art von Tabelle konstruiert werden, die einer anderen Berechnungsvorschrift folgt. Dabei wird es nicht darum gehen, wie aus den Spielen die Ergebnisse wurden, sondern nur darum, wie man mit den Endergebnissen umgeht. Genau so wie die Tabelle auf nichts anderem als den Resultaten fußt, wird in diesem Artikel keine andere Größe herangezogen: kein Chancenverhältnis, kein Marktwert, keine Zuschauerzahl. Es soll eine bessere Rangordnung der Mannschaften entstehen, ohne sich damit zu befassen, was über das Endergebnis hinaus auf den Plätzen passiert ist.
Herauskommen soll trotzdem eine treffendere Einschätzung der bisher erbrachten Leistungen als es die Tabelle zum aktuellen Zeitpunkt ist. Der erste Kritikpunkt wird dabei bestehen bleiben – Abschlussglück oder Formschwäche wirken sich auf dem Platz aus, beeinflussen das Ergebnis. Am zweiten lässt sich arbeiten. Die erspielten Ergebnisse sollten nicht alle gleich behandelt werden, sondern differenziert anhand der Gegner bewertet. Am einfachsten ist dies, indem man die Punktzahlen der bisherigen Gegner addiert.
Eine ganz einfache Umsetzung: Auf der Hochachse finden sich die erzielten Punkte, auf der Rechtsachse sind die erzielten Punkte der bisherigen Gegner aufsummiert. Wer oben steht, steht auch in der Tabelle oben; wer rechts steht, hatte Gegner, die im Schnitt weit oben stehen. Es lässt sich also mit einigem Recht behaupten, dass Hannover und Augsburg, obwohl sie beide gleich viele Punkte erspielt haben, bislang unterschiedlich starke Gegner hatten und Augsburg, das gegen schwerere Gegner dieselbe Punktzahl erreicht hat, stärker als Hannover einzuschätzen ist. Mehr noch: Der VfL Wolfsburg scheint um Welten stärkere Gegner als Hertha BSC erwischt zu haben, hat dabei aber trotzdem nur zwei Punkte weniger erreicht – sollte das nicht Grund genug sein, den VfL ohne Ansehen des Kaders für stärker als die Hertha zu halten?
Man könnte nun einfach so verfahren, Bonuspunkte anhand der Punktesumme der bisherigen Gegner zu vergeben. Neben der Frage, wie die Anzahl dieser Bonuspunkte berechnet werden sollten, ergibt sich dabei ein großes Problem: Wolfsburg hat weniger Punkte erreicht als die Hertha, selbst wenn der VfL also nach Ermittlung der Bonuspunkte vor der Hertha läge, hätten die anderen Teams immer noch für einen Sieg gegen Wolfsburg weniger Bonus kassiert als für einen Sieg gegen die Hertha – was das Anliegen konterkarieren würde.
Es braucht also ein System, um all diese Korrekturen auf einmal und in einem angemessenen Ausmaß durchzuführen. Das ist nicht allzu kompliziert zu bewerkstelligen, die Beschreibung der mathematischen Umsetzung passt in den folgenden Absatz, wer daran nicht interessiert ist, kann ihn überspringen und wird nicht weiter damit behelligt.
Man betrachte jede gespielte Partie als ein Nullsummenspiel, bei dem ingesamt 2 Punkte vergeben wurden. Nun lässt sich jedem Team eine Variable zuweisen, die angibt, wie viele Punkte es gegen einen gedacht neutralen Gegner durchschnittlich erspielt. Hat jedes Team eine solche Variable, lässt sich für den Ausgang jedes Spiels ein erwartungswertartiges E‘ ansetzen: Es liegt bei dem neutralen einen Punkt, plusminus Heimvorteil, plus der eigenen Variable, minus der Variable des Gegners. Ein gedacht neutraler Gegner hätte die Variable 1, E‘ läge bei der eigenen Variable plusminus Heimvorteil. Um die Variablen zu bestimmen, reicht ein weiterer Gedankenschritt: Summiert man diese E‘ über alle gespielten Spieltage auf, sollte in der Summe die tatsächliche Punktzahl nach der 2-Punkte-Tabelle herauskommen. Damit bleibt der Rest Formsache: Alle solchen Gleichungen für die 18 Mannschaften ergeben zusammen ein lineares Gleichungssystem aus einer 18×18-Matrix, die davon abhängt, welche Spiele absolviert wurden und einer rechten Seite, die aus den Ergebnissen ermittelt wird. Die Lösung des LGS ist ein Vektor aus den 18 Variablen für die einzelnen Teams. Diese Werte lassen sich (unter Berücksichtigung des Remisanteils der Liga) wieder zu Punktzahlen skalieren, die mit den tatsächlich erreichten Punkten verglichen werden können:
Die dynamische Tabelle nach acht Spieltagen
Ich habe diese neue Tabelle, die nach den korrigierten, um die Auswirkung der Gegnerstärke bereinigten Punktzahlen erstellt wurde, mit dynamische Tabelle überschrieben. Warum das? Am Freitagabend steht das Spiel Mainz – Dortmund an. Vergleichen wir die Auswirkungen eines denkbaren Mainzer Sieges auf die Tabellen. In der klassischen Tabelle erhielte Mainz 3 Punkte, Dortmund keinen, fertig.
In der dynamischen Tabelle passiert mehr: Jedes Ergebnis hat Auswirkungen auf alle anderen Mannschaften. Natürlich gewinnt zunächst einmal Mainz Punkte hinzu. Weil Mainz aber angesichts eine Sieges gegen den BVB stärker einzuschätzen ist, wirkt sich dies positiv für jene Mannschaften aus, die Mainz geschlagen haben: So gewinnt etwa Schalke für ihren Sieg gegen Mainz nachträglich 0,2 Punkte hinzu. Eine Niederlage gegen Dortmund hingegen scheint nicht mehr so »unvermeidbar« wie vorher, die Hertha verliert deswegen 0,1 Punkte. Diese Veränderungen bei Schalke und Hertha sorgen wiederum für minimale Veränderungen bei deren Gegnern (usw) und so ist die gesamte Tabelle in Bewegung.
Die neue Tabelle ist also dynamisch, weil sie die Liga als ein zusammenhängendes System auffasst. Anhand von Einzelergebnissen trifft sie Aussagen über die gesamte Liga, auch über scheinbar unbeteiligte Mannschaften – im Gegensatz zur klassischen Tabelle, in der sich jedes Spiel nur zwischen den zwei Teams abspielt, während die Wertung der anderen Mannschaften statisch und unberührt bleibt. Das folgende Diagramm zeigt einen Vergleich der aktuellen Punktzahlen mit den bereinigten Punktzahlen der dynamischen Tabelle.
Zur Erläuterung: Wiederum ist die klassische Punktzahl auf der Hochachse eingetragen, die bereinigte Wertung in der dynamischen Tabelle findet sich auf der Rechtsachse. Die eingezeichnete Diagonale ist die Gerade, auf der die Wertung in beiden Tabellen übereinstimmt. Ziemlich genau auf ihr finden sich Dortmund und Köln, bei denen klassische und dynamische Tabelle nahezu übereinstimmen.
Teams, die oberhalb der Diagonalen liegen, haben in der dynamischen Tabelle eine niedrigere Punktzahl als in der klassischen. Im Falle des FC Bayern liegt dies hauptsächlich daran, dass er schon deswegen ein leichtes Gegnerprogramm hatte, weil er nicht gegen sich selbst spielen musste. Ansonsten sei hierbei besonders der FC Schalke 04 hervorgehoben (bisher gegen Wolfsburg, Köln, Mainz, Darmstadt, Hamburg, Frankfurt, Bremen, Stuttgart).
Teams, die unterhalb der Diagonalen liegen, haben in der dynamischen Tabelle eine höhere Punktzahl als in der klassischen – ein Beispiel dafür ist Darmstadt (bisher gegen Bayern, Dortmund, Schalke, Leverkusen, Mainz, Hoffenheim, Bremen, Hannover). Eine weitere interessante Beobachtung: In der dynamischen Tabelle findet sich zwischen Frankfurt und Gladbach eine klare Abtrennung des Tabellenmittelfelds vom Tabellenkeller (links im Diagramm) – in der klassischen Tabelle sind diese beiden Teams punktgleich.
Es soll nicht unter den Tisch gekehrt werden, dass ein Teil der Veränderungen durch eine bloße Anwendung der 2-Punkte-Regel in die ähnliche Richtung geht, weil dadurch Unentschieden mehr und Siege weniger wertvoll werden. Dass die dynamische Tabelle aber weit mehr als eine 2-Punkte-Tabelle ist, zeigt etwa ein Blick auf das Trio Hertha-Köln-Ingolstadt: alle drei weisen die Bilanz 4 Siege, 2 Remis, 2 Niederlagen und damit nach 2- und 3-Punkte-Regel dieselbe Punktzahl auf, die Unterschiede von mehr als einem Punkt in der dynamischen Tabelle sind also allein dem Gegnerprogramm geschuldet, das »Doch!« aus der Einleitung ist umgesetzt.
Die dynamische Tabelle ist also eine Möglichkeit, aus nichts weiter als den Ergebnissen der gespielten Partien eine Rangfolge der Mannschaften zu erstellen, die unterschiedlich starke Gegner nicht ignoriert. Dass die entsprechenden Korrekturen relativ gering ausfallen, ist ein Anhaltspunkt dafür, diesen Kritikpunkt an der klassischen Tabelle als nicht allzu gravierend zu bewerten.
Dabei ist die dynamische Tabelle in der jetzigen Saisonphase aussagekräftiger, die Abweichungen von der klassischen Tabelle mutmaßlich größer als zu irgendeinem anderen Zeitpunkt der Saison. In diesen Wochen sind die Gegnerprogramme maximal durchmischt. Dies kann man sich leicht klar machen: nach dem 1. Spieltag haben Team A und B gegen jeweils einen – unterschiedlichen – Gegner gespielt. Nach 17 Spieltagen sind sie jeweils gegen 17 Gegner angetreten – von denen 16 identisch sind. Je weiter ein Spieltag von diesen Extremen 1 und 17 entfernt ist, desto größer kann der Unterschied zwischen den Gegnerprogrammen von A und B werden; das Maximum sind 9 Unterschiede. Der achte Spieltag ist der einzige, an dem zwei Teams komplett unterschiedliche Gegnerprogramme aufweisen und dabei gemeinsam die gesamte Liga umfassen können:
Köln spielte gegen Schalke, Wolfsburg, Ingolstadt, Hertha, Hamburg, Frankfurt, Gladbach und Stuttgart. Leverkusen spielte gegen Bayern, Dortmund, Mainz, Darmstadt, Hoffenheim, Bremen, Augsburg und Hannover.
Oder auch:
Hertha spielte gegen Dortmund, Wolfsburg, Köln, Hamburg, Frankfurt, Bremen, Augsburg und Stuttgart. Mainz spielte gegen Bayern, Schalke, Ingolstadt, Leverkusen, Darmstadt, Gladbach, Hoffenheim und Hannover.
Und ohne dass ich im Einzelnen weiß, mit welchen Algorithmen und welcher Eingriffnahme der Spielplan der Bundesliga entsteht – dass solche Gegnerprogramme nach acht Spieltagen alles in allem beeindruckend fair verteilt sind und niemand von sich behaupten kann, ein gravierend schwierigeres Programm als ein Konkurrent gehabt zu haben, dass also die dynamische Tabelle nah an der klassischen liegt, spricht sicherlich auch für die Spielplanerstellung der DFL.





Lustig das da noch mehr menschen drauf kommen;) Find ich aber gut.
Das ist ein cleverer Gedanke, in den Amerikanischen Sportarten (insbesondere College) sind derartige betrachtungsweisen mehr oder weniger Standard, weil ja meist am Ende keine Tabelle wie in der Bundesliga rauskommt, und ja garnicht jeder gegen jeden spielt.
Da die Punktsumme für jede Mannschaft sich nach schritt 1 ja geändert hat kann man da also ein schönes Gleichungssystem aufmachen(das sich von Hand eher nicht lösen lässt).
Da kommt dann sowas wie das SRS raus:
http://www.pro-football-reference.com/blog/?p=37
Das Analoge zum Point-spread wären Tordifferenzen. Das habe ich nach dem 5. Spieltag mal durchgerechnet, weil ich damals wissen wollte ob es Leverkusen hilft. (hier in alphabetischer Reihenfolge)
1,002944273 Augsburg
-0,367089496 Hertha
-3,635797203 Bremen
-3,379189844 Darmstadt
11,28618284 Dortmund
5,290207657 Frankfurt
-2,640154139 Hamburg
-7,028099156 Hannover
-6,226080589 Hoffenheim
2,184685203 Ingolstadt
-1,422974459 Köln
-4,082433918 Leverkusen
0,032000865 Mainz
-9,276148418 Gladbach
9,935017157 München
0,505647285 Schalke
-7,72687263 Stuttgart
7,238095238 Wolfsburg
Matlab-Simulation by TW von SV.de. Danke nochmal.
Danke für den Link – das ist tatsächlich dieselbe, wohl naheliegende Idee. Den Gedanken, Tordifferenzen anstelle der Tendenzen zu verwenden, habe ich aus zwei Gründen verworfen:
1. Es wird seitens der Mannschaften nicht auf Tordifferenz, sondern auf Tendenz gespielt, in Führung liegend wird die Ausrichtung im Allgemeinen defensiver; die gewünschte Leistung, die Zielsetzung auf dem Platz liegt nicht in der Optimierung der Tordifferenzen, sondern in der Optimierung der Punktzahl. Bei einem Tor Vorsprung wird der Zugewinn eines zusätzlichen Tores als viel weniger gravierend als das Erleiden des Ausgleichs behandelt. Die Tordifferenz behandelt beides gleich.
2. Die Tordifferenz, so spielübergreifend, wie sie hier eingehen würde, ist, selbst wenn es der angestrebte Wert wäre, in meiner Wahrnehmung viel schwankender und mit deutlicheren Ausreißern gespickt (Frankfurt +4 Köln) als es einer längerfristigen, besonnenen Bewertung der Mannschaften gut täte.
Gegenüber diesen beiden Kritikpunkten erscheint mir der Nachteil der reinen Tendenzen, die ausgedrückte Deutlichkeit einer Überlegenheit zu ignorieren, erträglich.
Steht ja auch im verlinkten Artikel das SRS zu defensiv agierenden Teams eher unfair sind.
Tordifferenzen produzieren auf dauer größere abstände und das will man ja eigentlich haben, denn dann kann man besser differenzieren. Wenn du nur Punkte verwendest kannst du garnicht so viel differenz „erarbeiten“. Is schon klar das die aktuelle und die bereinigte Punktzahl so nahe beisammenliegen.
In der Bundesliga wird sone tabelle ja auch immer uninteressanter, je länger die saison wird, weil zur Winterpause hat sich je jeder mit jedem getroffen dann in der Rückrunde die Strength of Schedule uninteressant. Also ist es für solche experimente wichtig das sie sehr früh funktionieren undd as geht mit der Tordifferenz einfach besser.
Außerdem sagt dir die Tordifferenz mehr über die Stärke einer Mannschaft als ihre Punkte ;)
Ich kann mich diesem Loblied auf die Tordifferenz nicht anschließen.
Ich schätze den Fußball ohne B-Note, bei dem es darum geht, mehr Tore als der Gegner zu schießen, egal ob man dabei defensiv oder offensiv agiert. Die 90 Minuten als Einheit des Spiels, an dessen Ende ein Sieger feststeht. Das Prinzip der Punkte, nach dem es wichtig ist, in möglichst vielen einzelnen Spielen mehr Tore als der jeweilige Gegner zu schießen, und weit weniger wichtig, ingesamt mehr Tore als Gegentore verbuchen zu können. Den Unterschied zwischen der Bilanz 1:0 1:0 1:0 0:3 und der Bilanz 3:0 0:1 0:1 0:1, den es nach der Tordifferenz überhaupt nicht gäbe. Den Anreiz, beim Stande von 0:2 alles nach vorne zu werfen, weil man das Spiel nicht aufgeben will und weil man nicht weniger als 0 Punkte bekommen kann, egal wie hoch man verliert. Die Endtabelle als eine Rangliste der Mannschaften, die all das berücksichtigt.
Ich wollte nur ein paar kleine Ungerechtigkeiten korrigieren, die sich im Laufe der Saison dabei einschleichen. Stärkebewertungen anhand der Tordifferenz vorzunehmen, mag seine Berechtigung haben, ist aber eine ganz andere Baustelle.
Wenn ich ne Stärkebewertung vornehmen will nehme ich mir irgendwas besseres als Punkte oder Tordifferenz. Eine der Shotmetriken zum Beispiel oder am liebsten ne verlässliche Quelle für Torchancen in jedem Spiel(gibts noch nicht öffentlich).
Ich habe die Tordifferenz hier vorgeschlagen, weil sie einfach unter den Bedingungen dieser Metrik einfach besser funktioniert, und sonst aus keinem anderen Grund.
Der letzte Satz war einfach eine freie Zusatzinformation.
Die ganzen Fringe-cornercases [z.B. 1:0 1:0 1:0 0:3] mit denen so gerne argumentiert wird ignoriert man besser das ist in der realität erschreckend selten relevant. Dem kann man meist mit komplexeren Modellen entgegewirken, aber es ist alles Frage des Aufwands.
Ob man eine sinnvolle Betrachtung angestellt hat, kann man doch am besten mit alten Daten vergleichen. Wenn man diese dynamische Tabelle eines 8. Spieltags mit der echten Tabelle dieses 8. Spieltag vergleicht, ist man dann näher an der Tabelle des 34. Spieltags jener Saison?
Ich vermute nicht. Denn schon sehr oft haben sich Mannschaften mitten in der Saison extrem verändert. Dortmund in der letzten Saison zum Beispiel. Und es gibt sicher noch viele andere Beispiele, wo um Weihnachten mal ein neuer Trainer kam und die Mannschaft dann plötzlich viel stärker war.
Wir haben so viele Tabellen, Ergebnisse und Statistiken. Vom Anbeginn der Zeit bis zum letzten Spieltag. Aber uns interessieren doch eigentlich nur die Ergebnisse des nächsten Spieltages.
Wie schon gesagt: Ich wollte in erster Linie keine Stärkeermittlung durchführen, sondern nur die bestehende Tabelle ein wenig korrigieren.
Der Vorschlag, die klassische und die dynamische Tabelle in Hinblick auf den 34. Spieltag zu vergleichen, ist trotzdem zumindest interessant. Ich habe also für einige Saisons die Tabellen (klassische und dynamische) nach dem 8. Spiel auf 34 Spieltage hochgerechnet und die Abweichungen von der tatschlichen Endtabelle gemessen (Summe der quadrierten Punktdifferenzen zwischen Prognose und Tatsache).
Die erste Spalte gibt die Saison an, dann folgt die Abweichung für die klassische Tabelle, dann die Abweichung für die dynamische Tabelle, und schließlich, um wie viel Prozent der Fehler der dynamischen Tabelle kleiner ist, also um wie viel besser die dynamische Tabelle die Endtabelle vorausgesagt hat.
2014-15 2841 3550 -24%
2013-14 2592 2005 22%
2012-13 2782 2134 23%
2011-12 3292 2909 11%
2010-11 4970 3773 24%
2009-10 4045 3023 25%
2008-09 1885 1192 36%
2007-08 1779 1890 -6%
2006-07 3013 2195 27%
2005-06 2733 1956 28%
2004-05 4455 3889 12%
2003-04 2748 1743 36%
2002-03 2168 2179 0%
2001-02 (kein Ergebnis, vmtl ein Fehler in der Datenbank)
2000-01 1767 2064 -16%
1999-00 2926 2491 14%
1998-99 4701 3263 30%
1997-98 2137 1711 19%
1996-97 3055 3016 1%
1995-96 3196 3258 -1%
In 14 von 19 Spielzeiten seit Einführung der 3-Punkte-Regel war die dynamische Tabelle nach 8 Spieltagen näher an der Endtabelle als die klassische.
[Update: in 14, nicht in 15. die 0% 2002-03 sind knapp negativ.]
Neu ist die Überlegung ja nicht. In den Nordamerikanischen Ligen wird das bei MLB, NBA, NFL unter Strength of Schedule erfasst. Da ist es insbesondere auch deshalb interessant, weil im Gegensatz zur Bundesliga am Saisonende nicht unbedingt jeder gegen jeden gleich oft gespielt hat. D.h. in den 3 Ligen unterscheidet sich eben der SoS auch am Saisonende zum Teil erheblich. In der NBA ist das noch am ausgeglichensten, weil bei den 82 Partien 2-4 mal gegen jedes andere Team angetreten wird. In der NFL ist das bei 16 Partien und 32 Teams ohnehin klar, dass nicht jeder gegen jeden wenigstens einmal antreten kann. Und auch Baseball (MLB) tritt trotz 162 Saisonspielen nicht jeder gegen jeden an: Zwischen American League und National League gibt relativ wenige Partien.
Danke für die Quervergleiche zu den amerikanischen Ligen. Mir waren »Strength of Schedule« und die damit verbundenen Berechnungen nicht bekannt. Der Ansatz, auf den ich gekommen bin, scheint angesichts dieses bereits etablierten Konzeptes also einerseits schon vor mir umgesetzt worden, andererseits aber immerhin keine schlechte Idee zu sein.
Guter Ansatz. Leider verstehe ich deine Erklärung nicht ganz:
„plusminus Heimvorteil“
Ist das eine Konstante? Oder ergibt sich die aus der Lösung des LGS (das wäre doch dann aber eine Variable zuviel…)
Vor dem ersten Spieltag ist der Erwartungswertes jedes Spieles also
1 +- Heimvorteil + 0 – 0
? Also Remis mit leichter Chance auf Heimsieg?
Der Heimvorteil ist hier ein konstanter Punktewert, den ich aus den vergangenen Jahren in der Bundesliga gemittelt habe – im Schnitt holten die Heimteams nach 2-Punkte-Regel etwa 7/12, die Auswärtsteams 5/12 der Punkte, 1x»Heimvorteil« sind also ein Sechstel Punkt.
Für ein Spiel zweier gleich starker Teams wäre also das Ergebnis 7/6 : 5/6 (Nach Punkten, nicht Toren) dasjenige, das am nächsten an den bestehenden Werten der Variablen liegt – wie in deinem Beispiel vor dem ersten Spieltag.
Mit der Berechnung von Prognosen, speziell von »Erwartungswerten« aus diesem LGS muss man aber vorsichtig sein: Trifft ein starkes Team mit einer Variablen von 1,5 nach den bisher absolvierten Spielen daheim auf eines mit der Variablen 0,5 –dann wäre der »Erwartungswert« ja 1 +Heimvorteil +1,5 -0,5 = 2 +Heimvorteil, also größer als die überhaupt zu erreichende Punktzahl. Der Begriff »erwartungswertartig« soll nur die Vorstellung dafür, was im LGS passiert, schärfen, eine belastbare Bezeichnung im Sinne der Stochastik ist es nicht.